ÍNDICE:
ToggleConectivas lógicas ou Operadores lógicos
As conectivas lógicas, também conhecidas como operadores lógicos, são partículas que representam diferentes operações lógicas.
Assim como na aritmética elementar, onde os símbolos de adição (+), subtração (-), multiplicação (x) e divisão (÷) representam diferentes operações matemáticas sobre números, as partículas como negação (¬), conjunção (∧), disjunção (∨), condicional (→) e bicondicional (↔) representam diferentes operações sobre valores de verdade na lógica proposicional.
Negação (¬)
Negação (¬): Representa a operação de negar uma proposição, ou seja, inverter seu valor de verdade.
A negação (¬ ou ~) é um operador lógico que, ao ser aplicado a uma única proposição, a torna falsa se for verdadeira e verdadeira se for falsa. Por exemplo, se considerarmos verdadeira a proposição “Lurdes Mutola é atleta moçambicana”, então a proposição “Lurdes Mutola não é atleta moçambicana” será falsa, pois é a negação da primeira.
A negação é uma função de verdade, pois basta saber se uma proposição qualquer p é verdadeira ou falsa para determinar o valor de verdade da nova proposição ¬p.
Como uma proposição pode ter dois valores de verdade – verdadeiro (V ou 1) e falso (F ou 0) – e o valor lógico de cada proposição composta depende dos valores lógicos das proposições simples que a compõem, é possível construir uma tabela de verdade para a negação, relacionando os possíveis valores de verdade para a proposição p e sua negação, ¬p.

Conjunção (∧)
Conjunção (∧): Representa a operação de conjunção, onde duas proposições são conectadas e ambas devem ser verdadeiras para que a conjunção seja verdadeira.
A conjunção (∧ ou & ou .) é uma operação lógica que conecta duas ou mais proposições simples ou atômicas para formar uma nova proposição composta. Por exemplo, consideremos as proposições “Mataka está doente” e “Mataka vai ao médico”, que podem ser simbolizadas pelas variáveis p e q. Ao combinar essas proposições usando o conector de conjunção (∧), obtemos a nova proposição “Mataka está doente e vai ao médico”.
A conjunção é representada pelo símbolo ∧ (ou & ou .) e a proposição resultante, “Mataka está doente e vai ao médico”, pode ser escrita como p ∧ q (podendo ser lida como “p e q”). A conjunção é verdadeira somente se ambas as proposições forem verdadeiras. Basta que uma das proposições seja falsa para que a conjunção seja falsa.
Se as proposições “Mataka está doente” e “Mataka vai ao médico” forem verdadeiras, então a proposição “Mataka está doente e vai ao médico” também será verdadeira. A tabela a seguir mostra em quais condições a conjunção é verdadeira.

Disjunção (∨)
Disjunção (∨): Representa a operação de disjunção, onde duas proposições são conectadas e pelo menos uma delas deve ser verdadeira para que a disjunção seja verdadeira.
A disjunção (V) é a operação que expressa uma alternativa, sendo traduzida na linguagem comum pela partícula “ou” e, na lógica matemática, pelo símbolo V. Existem dois tipos de disjunção:
Disjunção Inclusiva (V)
Disjunção inclusiva: Na linguagem comum, é identificada pela expressão “e/ou” e representada pelo símbolo V (no sentido inclusivo). A disjunção inclusiva é falsa quando ambas as proposições que a compõem são falsas.
Basta que uma das proposições simples seja verdadeira para que a disjunção inclusiva seja verdadeira. Por exemplo, a proposição “Este sol ou a temperatura está agradável” é verdadeira em determinadas situações.

Disjunção Exclusiva (V- ou W)
Disjunção exclusiva (V- ou W): É considerada exclusiva quando as proposições simples que a compõem se excluem mutuamente, ou seja, a verdade de uma implica necessariamente a falsidade da outra. A proposição pvq é verdadeira se p e q tiverem valores distintos e é falsa nos outros casos.
Por exemplo, a proposição “Estou vivo ou estou morto” não permite que as proposições atômicas ou simples sejam simultaneamente verdadeiras.
A disjunção exclusiva é simbolizada por V ou por VV. Por exemplo, a proposição “Adija passou de classe ou reprovou” significa que Adija passou de classe ou reprovou, mas não pode ter passado de classe e reprovado ao mesmo tempo.
Assim, a estrutura da proposição pode ser destacada, distinguindo as conectivas e as proposições, como em “(Adija passou de classe V reprovou) A – (pode ter passado A reprovado)”. Simbolizando, temos (pVq) A – (p^q), ou ainda, (pVVq).

Condicional ou Implicação (→)
Condicional (→): Representa a operação de implicação, onde uma proposição implica na outra, ou seja, se a primeira for verdadeira, então a segunda também deve ser verdadeira.
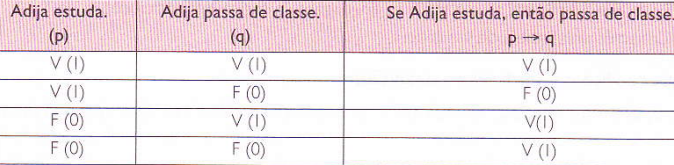
A condicional ou implicação (-) é uma operação lógica que relaciona duas proposições (p e q) através da expressão “se… então…”, formando uma proposição composta condicional. Por exemplo, “Se Adija estuda, então passa de classe” é simbolizado por p→q, podendo ser lido como “se p, então q”.
Neste caso, a proposição “p” é chamada de antecedente ou condição (ou hipótese), enquanto a proposição “q” é chamada de consequente ou condicionado (ou conclusão).
Na implicação, se a proposição “p”, o antecedente, for verdadeira, então a proposição “q”, o consequente, também será verdadeira, uma vez que a fórmula “p→q” significa que não há “p”. Dessa forma, a implicação só é falsa quando o antecedente é verdadeiro e o consequente é falso.
Bicondicional ou Equivalência(↔)
Bicondicional (↔): Representa a operação de equivalência, onde duas proposições são equivalentes, ou seja, possuem o mesmo valor de verdade em todas as situações.
O bicondicional ou equivalência (↔) é uma operação lógica que relaciona duas proposições atômicas (simples) através da expressão “se e somente se”, simbolizada por p↔q. A equivalência é verdadeira quando as proposições p e q têm o mesmo valor lógico e é falsa quando possuem valores lógicos diferentes. Por exemplo, a proposição “x é par se e somente se x é divisível por 2” é representada por p↔q, onde p é “x é par” e q é “x é divisível por 2”.

Essas conectivas lógicas possuem expressões verbais e símbolos específicos para representar cada operação lógica, facilitando a análise e manipulação de proposições na lógica proposicional.
Artigos “Lógica II“
Confira estes artigos:
-
Conectivas lógicas ou Operadores lógicos
As conectivas lógicas, também conhecidas como operadores lógicos, são partículas que representam diferentes operações lógicas.
-
Proposições simples e proposições complexas
Este artigo aborda a distinção entre Proposições simples e proposições complexas, explorando sua importância na…
-
A Lógica Proposicional ou Lógica moderna
A lógica proposicional, também conhecida como lógica sentencial, é um ramo da lógica que se…
-
Falácias: conceito, caraterísticas e tipos
Falácia é o termo utilizado para um raciocínio errado que aparenta ser verdadeiro. A origem…
-
Silogismos hipotéticos: condicional, disjuntivo, conjuntivo e dilema
Silogismos hipotéticos são um tipo de silogismo que, ao contrário dos silogismos categóricos, têm a…
-
Classificação dos silogismos
Classificação dos silogismos – Existem dois tipos principais de silogismo: categóricos e hipotéticos
-
Figuras e modos do silogismo
A figura de um silogismo é determinada pelo papel que o termo médio desempenha nas…
-
Silogismo: conceito, estrutura, princípios e regras
O silogismo é uma forma de inferência mediata ou raciocínio dedutivo, desenvolvido por Aristóteles na…
-
Inferências Mediatas (ou Raciocínios)
-Analogia, indução e dedução são três tipos de inferências mediatas ou raciocínios completamente diferenciados. saiba…
-
Inferências Imediatas por Conversão
Inferências imediatas por conversão são um tipo de operação lógica em que as proposições são…


