Figuras e modos do silogismo

Figuras e modos do silogismo: O que determina a figura de um silogismo?

A figura de um silogismo é determinada pelo papel que o termo médio desempenha nas duas premissas, seja como sujeito numa e predicado na outra, ou como predicado numa e sujeito na outra, ou ainda como predicado ou sujeito em ambas as premissas. Dessa forma, existem quatro figuras possíveis.

1.ª Figura (sub-prae)

Ao analisar o seguinte silogismo, observe o que ocorreu com o termo médio nas premissas apresentadas:
Todo homem é mortal.
Ofélia mata homem.
Então, Ofélia é mortal.
Nesta figura, o termo médio “homem” é sujeito na premissa maior e predicado na premissa menor.

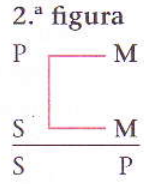
2.ª Figura (prae-prae)

Ao considerar o seguinte silogismo, identifique o que aconteceu com o termo médio contido nas premissas:
Os angolanos não são adeptos de Mogambola.
Ora, os moçambicanos são adeptos de Moçambola.
Logo, os angolanos não são adeptos.
O termo médio “adeptos de Moçambola” é predicado em ambas as premissas.

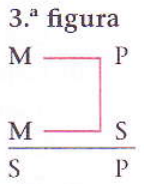
3.ª Figura (sub-sub)

Analisando o silogismo a seguir, descubra o que ocorreu com o termo médio presente nas premissas:
Os batráquios não comem cenouras.
Os batráquios são anfíbios.
Portanto, os anfíbios não comem cenouras.
O termo médio “batráquios” é sujeito em ambas as premissas, ao contrário da segunda figura.

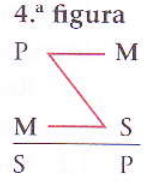
4.ª Figura (prae-sub)

Ao analisar o seguinte silogismo, observe o que aconteceu com o termo médio contido nas premissas:
As hienas são animais quadrúpedes.
Os animais quadrúpedes são ferozes predadores.
Não há tigre que seja tão veloz como a hiena.
Nesta figura, o termo médio “animais quadrúpedes” é contraditório e está presente na premissa menor.

Como se forma o modo de um silogismo?

O modo do silogismo é a forma como os diferentes tipos de proposições (A, I, O, E) nele se dispõem. Fazendo combinações possíveis das quatro letras em grupos de três (que é o número de proposições de um silogismo categórico), temos 64 modos possíveis de silogismo.

Além disso, combinando as quatro figuras com os 64 modos, obtemos 256 silogismos. No entanto, apenas 19 são considerados modos válidos, aqueles que obedecem às 8 regras estabelecidas anteriormente. Vamos agora observar o quadro com os 19 modos válidos.

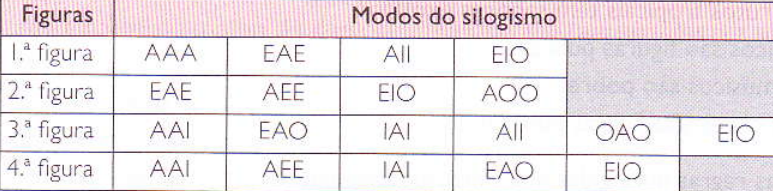
Através de vários procedimentos, sendo o mais importante a conversão, é possível reduzir silogismos de uma figura para outra.

Exemplos:
Nenhum maconde é ignorante.
Alguns políticos são ignorantes.
Alguns políticos não são macondes.

Nenhum ignorante é maconde.
Alguns políticos são ignorantes.
Alguns políticos não são macondes.

Nos exemplos dados, pode-se observar que, no primeiro silogismo, o termo médio “ignorante” desempenha a função de predicado nas duas premissas – trata-se de um silogismo do modo IIO. Convertendo a premissa maior do mesmo silogismo, podemos transformá-lo em um silogismo categórico da primeira figura, modo UO, onde o termo médio desempenha a função de sujeito.

Artigos “Lógica II“